齐次坐标系的理解
在计算机图形学里面会经常碰到几何体的平移,旋转,缩放以及投影变换. 一般情况下会涉及到齐次坐标与变换矩阵. 为了后续对变换矩阵内容的讲解, 在这里先简要的介绍一下什么是齐次坐标.
提出问题
两条平行线可以相交吗?
在欧氏空间(几何学)中,同一平面上的两条平行线不能相交,或者说不能永远相交。这是一个大家都熟悉的常识。
但是,在投影空间中就不一样了,比如,下图上的火车铁路在远离眼睛的时候会变得更窄。最后,两条平行的铁轨在地平线处相交,也就是无限远处的一点。
 铁路变窄,在地平线处相交
铁路变窄,在地平线处相交
欧氏空间(或笛卡尔空间)能很好地描述我们的2D/3D几何,但它们不足以处理投影空间(实际上,欧氏几何是投影几何的一个子集)。一个2D点的笛卡尔坐标可以表示为\((x,y)\)。
如果这个点远去到无穷远呢?无穷远处的点在欧氏空间中无法具体展示。在投影空间中,平行线会在无穷远处相遇,但在欧氏空间中却做不到。
解决方法
由 August Ferdinand Möbius(不错,就是那个莫比乌斯圈的那位) 提出的齐次坐标,使图形和几何学的计算在投影空间中成为可能。齐次坐标是用\(N+1\)个数来表示N维坐标的一种方式。
要制作二维齐次坐标,我们只需在现有坐标中增加一个额外的变量w。因此,笛卡尔坐标中的一点,\((X,Y)\)在齐次坐标中就变成了\((x,y,w)\)。而笛卡儿坐标中的X和Y在齐次坐标中的\(x\)、\(y\)和\(w\)则重新表达为
\[ \begin{aligned} X = \frac{x}{w} \\ Y = \frac{y}{w} \end{aligned} \]
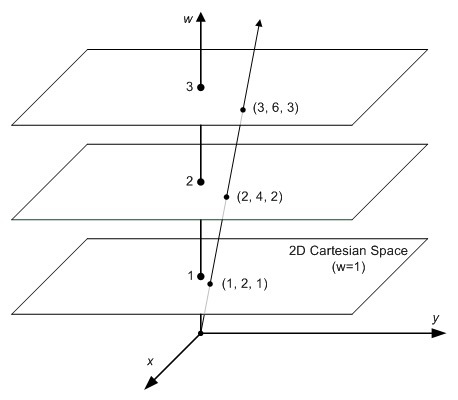
为什么叫 “齐次”呢? 如前所述,为了将齐次坐标\((x,y,w)\)转换为笛卡尔坐标,我们只需将\(x\)和\(y\)除以\(w\)即可。 \[ (x, y, w) \Leftrightarrow \Big(\frac{x}{w}, \frac{y}{w}\Big) \] 将Homogeneous转换为Cartesian,我们可以发现一个重要的事实。让我们看看下面的例子。 \[ \begin{aligned} Homogeneous& \quad Cartesian& \\ (1, 2, 3)\ &\Rightarrow \Big( \frac{1}{3}, \frac{2}{3} \Big)& \\ (2, 4, 6)\ &\Rightarrow \Big(\frac{2}{6}, \frac{4}{6} \Big)& &=\Big(\frac{1}{3}, \frac{2}{3}\Big) \\ (4, 8, 12)\ &\Rightarrow \Big(\frac{4}{12}, \frac{8}{12} \Big)& &=\Big(\frac{1}{3}, \frac{2}{3}\Big) \\ &\;\;\vdots \\ (1a, 2a, 3a)\ &\Rightarrow \Big(\frac{1a}{3a}, \frac{2a}{4a} \Big)& &=\Big(\frac{1}{3}, \frac{2}{3}\Big) \\ \end{aligned} \] 如你所见 \((1, 2, 3), (2, 4, 6)\)和\((4, 8, 12)\)这三个点对应于同一个欧氏点\((\frac{1}{3}, \frac{2}{3})\). 而任何乘以\(a\)的数\((1a,2a,3a)\)与欧氏空间中的\((\frac{1}{3},\frac{2}{3})\)是同一个点。因此,这些点是 “homogeneous/齐次 “的,因为它们在欧氏空间(或笛卡尔空间)中代表同一个点。换句话说,齐次坐标是与乘数\(a\)不相关的。
数学证明: 两条平行线可以相交
考虑以下欧氏空间的线性系统。 \[ \left \{ \begin{array}{c} Ax+By+C=0 \\ Ax+By+D=0 \end{array} \right. \]
而我们知道,由于C≠D,所以上述方程没有解。 如果C=D,那么两条线是相同的(重叠的)。
让我们重写投影空间的方程,将x和y分别替换为x/w,y/w。 \[ \left\{\begin{array}{l}A \frac{x}{w}+B \frac{y}{w}+C=0 \\ A \frac{x}{w}+B \frac{y}{w}+D=0\end{array} \quad \Rightarrow\left\{\begin{array}{l}A x+B y+C w=0 \\ A x+B y+D w=0\end{array}\right.\right. \] 现在,我们有一个解,\((x,y,0)\),因为\((C-D)w=0,\therefore w=0.\) 因此,两条平行线在\((x,y,0)\)处相交.
\((x,y,0)\)在几何上代表一条没有起点与终点, 也没有长度的射线,它只有方向。
齐次坐标的应用
齐次坐标在计算机图形学中是非常有用的基本概念,通过增加一个额外的维度\(W\)后,可以用来对几何体进行缩放,旋转,平移,透视投影的矩阵变换.
任何\(N\)维度齐次坐标,只要\(W\)不为\(0\),都可以通过将每一个分量除以\(W\)来转换到 \(W=1\)的向量, 然后获得其\(N-1\)维的欧式空间的点值。
而当\(W=0\)时,这个坐标表示无限长的一个向量,通常表示\(N-1\)维的矢量。